Additional Notes¶
Thanks for checking out my tutorial, I hope it was useful.
Stochastic Gradient Descent¶
Since in theano we use the theano.tensor.grad() to estimate gradients from errors and back propagate
ourselves, it was easier to understand and learn about various minimization algorithms. In yann for instance,
I had to write all the optimizers I used, by hand as seen
here.
In tensorflow everything is already provided to us in the Optimizer module.
I could have written out all the operations myself, but I copped out by using the in-built module.
Therefore, here is some notes on how to minimize an error.
Consider the prediction 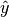 .
Consider we come up with some error
.
Consider we come up with some error  , that measure how different is
, that measure how different is 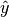 with
with 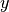 .
In our tutorial, we used the categorical cross-entropy error.
If
.
In our tutorial, we used the categorical cross-entropy error.
If  were a measure of error in this prediction, in order to learn any weight
were a measure of error in this prediction, in order to learn any weight 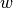 in the network,
we can acquire its gradient
in the network,
we can acquire its gradient 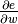 , for every weight
, for every weight 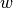 in the
network using the chain rule of differentiation.
Once we have this error gradient, we can iteratively learn the weights using the following
gradient descent update rule:
in the
network using the chain rule of differentiation.
Once we have this error gradient, we can iteratively learn the weights using the following
gradient descent update rule:
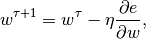
where, 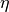 is some predefined rate of learning and
is some predefined rate of learning and 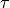 is the iteration number.
It can be clearly noticed in the back-prop strategy outlined above that the features of a CNN are
learnt with only one objective - to minimize the prediction error.
It is therefore to be expected that the features learnt thusly, are specific only to those particular tasks.
Paradoxically, in deep CNNs trained using large datasets, this is often not the typical observation.
is the iteration number.
It can be clearly noticed in the back-prop strategy outlined above that the features of a CNN are
learnt with only one objective - to minimize the prediction error.
It is therefore to be expected that the features learnt thusly, are specific only to those particular tasks.
Paradoxically, in deep CNNs trained using large datasets, this is often not the typical observation.
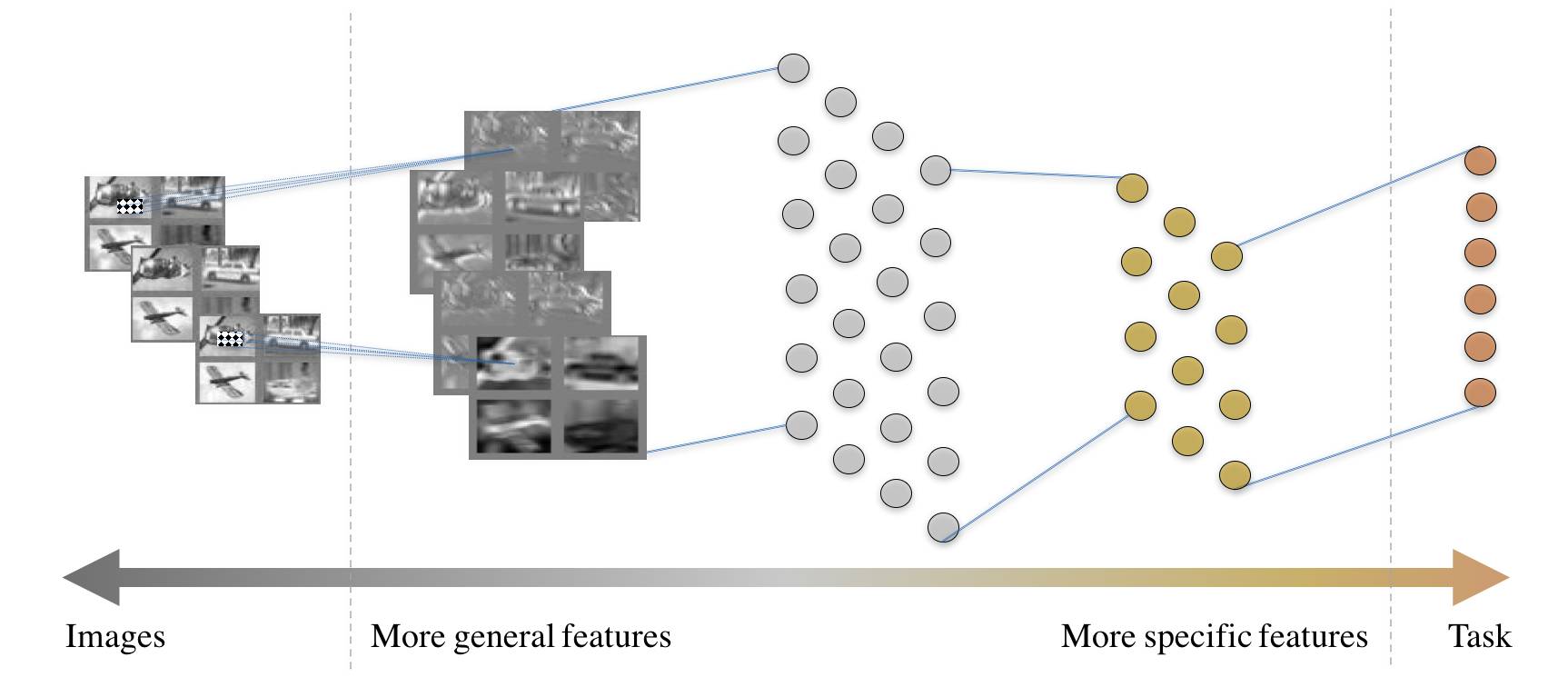
Fig. 12 The anatomy of a typical convolutional neural network.
In most CNNs, we observe as illustrated in the figure above, that the anatomy of the CNN and the ambition of each layer is contrived meticulously. The features that are close to the image layer are more general (such as edge detectors or Gabor filters) and those that are closer to the task layer are more task-specific.
Off-the-shelf Downloadable networks¶
Given this observation among most popular CNNs, modern day computer vision engineers prefer to
simply download off-the-shelf neural networks and fine-tune it for their task.
This process involves the following steps.
Consider that a stable network 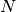 is well-trained on some task
is well-trained on some task 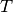 that has a large dataset
and compute available at site.
Consider that the target for an engineer is build a network
that has a large dataset
and compute available at site.
Consider that the target for an engineer is build a network 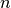 that can make inferences on task
that can make inferences on task 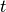 .
Also assume that these two tasks are somehow related, perhaps
.
Also assume that these two tasks are somehow related, perhaps 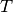 was visual object
categorization on ImageNet and
was visual object
categorization on ImageNet and 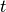 on the COCO dataset [LMB+14] or the Caltech-101/256
datasets [FFFP06].
To learn the task on
on the COCO dataset [LMB+14] or the Caltech-101/256
datasets [FFFP06].
To learn the task on 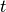 , one could simply download
, one could simply download 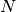 , randomly reinitialize the
last few layers (at the extreme case reinitialize only the softmax layer) and continue back-prop of
the network to learn the task
, randomly reinitialize the
last few layers (at the extreme case reinitialize only the softmax layer) and continue back-prop of
the network to learn the task 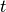 with a smaller eta.
It is expected that
with a smaller eta.
It is expected that 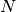 is very well-trained already that they could serve as good
initialization to begin fine-tuning the network for this new task.
In some cases where enough compute is not available to update all the weights, we may simply choose
to update only a few of the layers close to the task and leave the others as-is.
The first few layers that are not updated are now treated as feature extractors much the same way as HOG or SIFT.
is very well-trained already that they could serve as good
initialization to begin fine-tuning the network for this new task.
In some cases where enough compute is not available to update all the weights, we may simply choose
to update only a few of the layers close to the task and leave the others as-is.
The first few layers that are not updated are now treated as feature extractors much the same way as HOG or SIFT.
Some networks capitalized on this idea and created off-the-shelf downloadable networks that are designed specifically to work as feed-forward deterministic feature extractors. Popular off-the-shelf networks were the decaf [DJV+14] and the overfeat [SEZ+13]. Overfeat in particular was used for a wide-variety of tasks from pulmonary nodule detection in CT scans [vGSJC15] to detecting people in crowded scenes [SAN16]. While this has been shown to work to some degrees and has been used in practice constantly, it is not a perfect solution and some problems have known to exist. This problem is particularly striking when using a network trained on visual object categorization and fine-tuned for tasks in medical image.
Distillation from downloaded networks¶
Another concern with this philosophy of using off-the-shelf network as feature extractors is that
the network 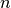 is also expected to be of the same size as
is also expected to be of the same size as 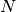 .
In some cases, we might desire a network of a different architecture.
One strategy to learn a different network using a pre-trained network is by using the idea of
distillation [HVD15], [BRMW15].
The idea of distillation works around the use of a temperature-raised softmax, defined as follows:
.
In some cases, we might desire a network of a different architecture.
One strategy to learn a different network using a pre-trained network is by using the idea of
distillation [HVD15], [BRMW15].
The idea of distillation works around the use of a temperature-raised softmax, defined as follows:
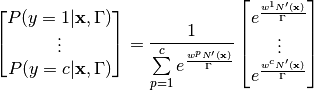
This temperature-raised softmax for 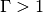 (
(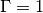 is simply the original
softmax) provides a softer target which is smoother across the labels.
It reduces the probability of the most probable label and provides rewards for the second and third
most probable labels also, by equalizing the distribution.
Using this dark-knowledge to create the errors
is simply the original
softmax) provides a softer target which is smoother across the labels.
It reduces the probability of the most probable label and provides rewards for the second and third
most probable labels also, by equalizing the distribution.
Using this dark-knowledge to create the errors  (in addition to the error over
predictions as discussed above), knowledge can be transferred from
(in addition to the error over
predictions as discussed above), knowledge can be transferred from 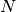 , during the training of
, during the training of 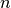 .
This idea can be used to learn different types of networks.
One can learn shallower [VL16] or deeper [RBK+14] networks
through this kind of mentoring.
.
This idea can be used to learn different types of networks.
One can learn shallower [VL16] or deeper [RBK+14] networks
through this kind of mentoring.